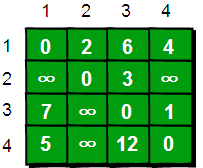
暑假,小哼准备去一些城市旅游.有些城市之间有公路,有些城市之间则没有,如下图.为了节省经费以及方便计划旅程,小哼希望在出发之前知道任意两个城市之前的最短路程.
上图中有4个城市8条公路,公路上的数字表示这条公路的长短.请注意这些公路是单向的.我们现在需要求任意两个城市之间的最短路程,也就是求任意两个点之间的最短路径.这个问题这也被称为“多源最短路径”问题.
现在需要一个数据结构来存储图的信息,我们仍然可以用一个4*4的矩阵(二维数组e)来存储.比如1号城市到2号城市的路程为2,则设e[1] [3]的值为2.2号城市无法到达4号城市,则设置e[2] [4]的值为∞.另外此处约定一个城市自己是到自己的也是0,例如e[1] [5]为0,具体如下.
我们来想一想,根据我们以往的经验,如果要让任意两点(例如从顶点a点到顶点b)之间的路程变短,只能引入第三个点(顶点k),并通过这个顶点k中转即a->k->b,才可能缩短原来从顶点a点到顶点b的路程.那么这个中转的顶点k是1~n中的哪个点呢?甚至有时候不只通过一个点,而是经过两个点或者更多点中转会更短,即a->k1->k2b->或者a->k1->k2…->k->i…->b.比如上图中从4号城市到3号城市(4->3)的路程e[4] [7]原本是12.如果只通过1号城市中转(4->1->3),路程将缩短为11(e[4] [1]+e[1] [3]=5+6=11).其实1号城市到3号城市也可以通过2号城市中转,使得1号到3号城市的路程缩短为5(e[1] [2]+e[2] [3]=2+3=5).所以如果同时经过1号和2号两个城市中转的话,从4号城市到3号城市的路程会进一步缩短为10.通过这个的例子,我们发现每个顶点都有可能使得另外两个顶点之间的路程变短.好,下面我们将这个问题一般化. 当任意两点之间不允许经过第三个点时,这些城市之间最短路程就是初始路程,如下.
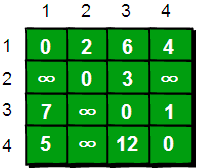
假如现在只允许经过1号顶点,求任意两点之间的最短路程,应该如何求呢?只需判断e[i] [1]+e[1] [j]是否比e[i] [j]要小即可.e[i] [j]表示的是从i号顶点到j号顶点之间的路程.e[i] [1]+e[1] [j]表示的是从i号顶点先到1号顶点,再从1号顶点到j号顶点的路程之和.其中i是1n循环,j也是1n循环,代码实现如下:
1 | for(i=1;i3->…->1->2->3这样路径中,每绕一次1->-2>3这样的环,最短路就会减少1,永远找不到最短路.其实如果一个图中带有“负权回路”那么这个图则没有最短路. |
我理解的Floyd算法原理:通过遍历每一个结点与其他所有结点可能存在的路径,取其中的最小值(通过遍历其他所有结点,使其充当中介结点与当前路径比较来实现),从而获得所有点之间的最短路径.原理说起来比较难懂,看前边的算法实现就明白了.
本文转自:傻子也能看懂的弗洛伊德算法(转) 侵删
本人水平有限,有错误的地方请指正,谢谢!